UPU
UPUOnline 2024/2025: Permohonan Lepasan SPM & STPM

Permohonan UPU Online Fasa 2 2023/2024 Mulai 15 Mei 2023

Contoh Soalan & Jawapan Peperiksaan MUET Yang Terkini

Pengambilan Kursus Program Kemahiran Hidup MAIK

Semakan Keputusan Rayuan UPUOnline Lepasan STPM 22/23

Intipati Bajet 2023 Berkaitan Pendidikan

Permohonan Biasiswa Yayasan Tan Sri Lee Loy Seng

Semakan Panggilan Temu Duga & Ujian Lepasan SPM Sesi 2022/2023

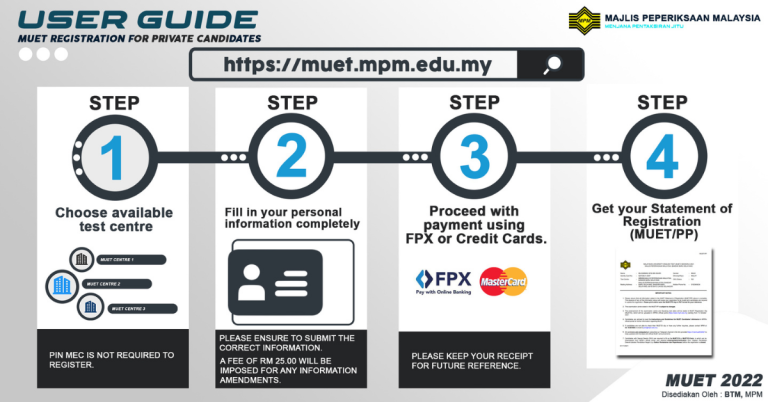
Daftar Peperiksaan MUET 2022: Malaysian University English Test